Category Archives: Research

The Quality of Postseason Play

Leave a reply

Summary: I look at averages for hitters and pitchers in the postseason to see how their quality (relative to league average) has changed over time. Unsurprisingly, the gap between postseason and regular season average pitchers is larger than the comparable gap for hitters. The trend over time for pitchers is expected, with a decrease in quality relative to league average from the 1900s to mid-1970s and a slight increase since then that appears to be linked with the increased usage of relievers. The trend for hitters is more confusing, with a dip from 1950 to approximately 1985 and an increase since then. Overall, however, the average quality of both batters and pitchers in the postseason relative to league average is as high as it has been in the expansion era.

Quality of play in the postseason is a common trope of baseball discussion. Between concerns about optics (you want casual fans to watch high quality baseball) and rewarding the best teams, there was a certain amount of handwringing about the number of teams with comparatively poor records into the playoffs (e.g., the Giants and Royals made up the only pair of World Series teams ever without a 90 game winner). This prompted me to wonder about the quality of the average players in the postseason and how that’s changed over time with the many changes in the game—increased competitive balance, different workloads for pitchers, changes in the run environment, etc.

For pitchers, I looked at weighted league-adjusted RA9, which I computed as follows:

  1. For each pitcher in the postseason, compute their Runs Allowed per 9 IP during the regular season. Lower is better, obviously.
  2. Take the average for each pitcher, weighted by the number of batters faced.
  3. Divide that average by the major league average RA9 that year.

You can think of this as the expected result you would get if you chose a random plate appearance during the playoffs and looked at the pitcher’s RA9. Four caveats here:

  1. By using RA9, this is a combined pitching/defense metric that really measures how much the average playoff team is suppressing runs relative to league average.
  2. This doesn’t adjust for park factors, largely because I thought that adjustment was more trouble than it was worth. I’m pretty sure the only effect that this has on aggregate is injecting some noise, though I’m not positive.
  3. I considered using projected RA9 instead of actual RA9, but after playing around with the historical Marcel projections at Baseball Heat Maps, I didn’t see any meaningful differences on aggregate.
  4. For simplicity’s sake, I used major league average rather than individual league average, which could influence some of the numbers in the pre-interleague play era.

When I plot that number over time, I get the following graph. The black dots are observed values, and the ugly blue line is a smoothed rolling estimate (using LOESS). (The gray is the confidence interval for the LOESS estimate.)

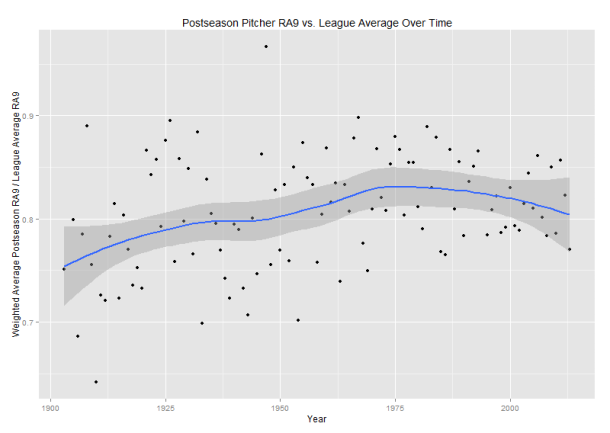
Pitching

While I wouldn’t put too much weight in the LOESS estimate (these numbers should be subject to a large bit of randomness), it’s pretty easy to come up with a basic explanation of why the curve looks the way it does. For the first seventy years of that chart, the top pitchers pitched ever smaller shares of the overall innings (except for an uptick in the 1960s), ceding those innings to lesser starters and dropping the average quality. However, starting in the 1970s, relievers have covered larger portions of innings (covered in this FiveThirtyEight piece), and since relievers are typically more effective on a rate basis than starters, that’s a reasonable explanation for the shape of the overall pitcher trend.

What about hitters? I did the same calculations for them, using wOBA instead of RA9 and excluding pitchers from both postseason and league average calculations. (Specifically, I used the static version of wOBA that doesn’t have different coefficients each year. The coefficients used are the ones in The Book.) Again, this includes no park adjustments and rolls the two leagues together for the league average calculation. Here’s what the chart looks like:

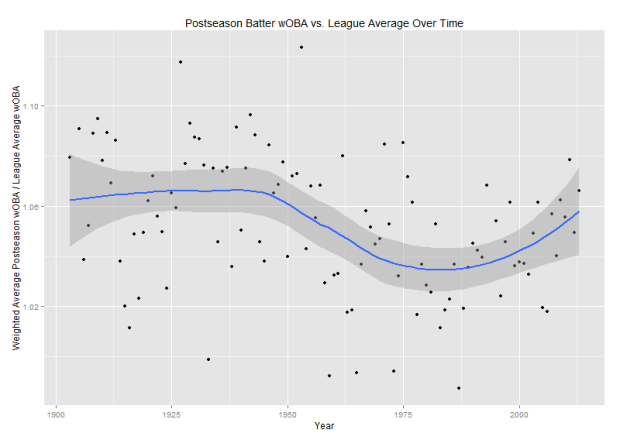
Batting

Now, for this one I have no good explanation for the trend curve. There’s a dip in batter quality starting around integration and a recovery starting around 1985. If you have ideas about why this might be happening, leave them in the comments or Twitter. (It’s also quite possible that the LOESS estimate is picking up something that isn’t really there.)

What’s the upshot of all of this? This is an exploratory post, so there’s no major underlying point, but from the plots I’m inclined to conclude that, relative to average, the quality of the typical player (both batter and pitcher) in the playoffs is as good as it’s been since expansion. (To be clear, this mostly refers to the 8 team playoff era of 1995–2011; the last few years aren’t enough to conclude anything about letting two more wild cards in for a single game.) I suspect a reason for that is that, while the looser postseason restrictions have made it easier for flawed teams to make it in the playoffs, they’ve also made it harder for very good teams to be excluded because of bad luck, which lifts the overall quality, a point raised in this recent Baseball Prospectus article by Sam Miller.

Two miscellaneous tidbits from the preparation of this article:

  • I used data from the Lahman database and Fangraphs for this article, which means there may be slight inconsistencies. For instance, there’s apparently an error in Lahman’s accounting for HBP in postseason games the last 5 years or so, which should have a negligible but non-zero effect on the results.
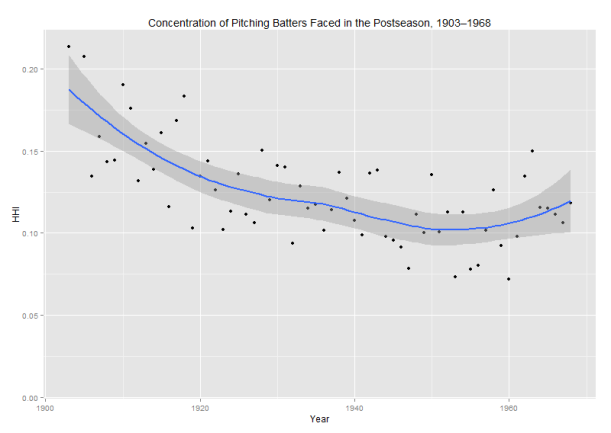
  • I mentioned that the share of batters faced in the postseason by the top pitchers has decreased steadily over time. I assessed that using the Herfindahl-Hirschman index (which I also used in an old post about pitchers’ repertoires.) The chart of the HHI for batters faced is included below. I cut the chart off at 1968 to exclude the divisional play era, which by doubling the number of teams decreased the level of concentration substantially.  HHI

Do Platoon Splits Mess Up Projections?

Leave a reply

Quick summary: I test the ZiPS and Marcel projection systems to see if their errors are larger for players with larger platoon splits. A first check says that they are not, though a more nuanced examination of the system remains to be conducted.

First, a couple housekeeping notes:

  • I will be giving a short talk at Saberseminar, which is a baseball research conference held in Boston in 10 days! If you’re there, you should go—I’ll be talking about how the strike zone changes depending on where and when games are played. Right now I’m scheduled for late Sunday afternoon.
  • Sorry for the lengthy gap between updates; work obligations plus some other commitments plus working on my talk have cut into my blogging time.

After the A’s went on their trading sprees last week at the trading deadline, there was much discussion about how they were going to intelligently deploy the rest of their roster to cover for the departure of Yoenis Cespedes. This is part of a larger pattern with the A’s as they continue to be very successful with their platoons and wringing lots of value out of their depth. Obviously, when people have tried to determine the impact of this trade, they’ve been relying on projections for each of the individual players involved.

What prompted my specific question is that Jonny Gomes is one of those helping to fill Cespedes’s shoes, and Gomes has very large platoon splits. (His career OPS is .874 against left-handed pitchers and .723 against righties.) The question is what proportion of Gomes’s plate appearances the projection systems assume will be against right handers; one might expect that if he is deployed more often against lefties than the system projects, he might beat the projections substantially.

Since Jonny Gomes in the second half of 2014 constitutes an extremely small sample, I decided to look at a bigger pool of players from the last few years and see if platoon splits correlated at all with a player beating (or missing) preseason projections. Specifically, I used the 2010, 2012, and 2013 ZiPS and Marcel projections (via the Baseball Projection Project, which doesn’t have 2011 ZiPS numbers).

A bit of background: ZiPS is the projection system developed by Dan Szymborski, and it’s one of the more widely used ones, if only because it’s available at FanGraphs and relatively easy to find there. Marcel is a very simple projection system developed by Tangotiger (it’s named after the monkey from Friends) that is sometimes used as a baseline for other projection systems. (More information on the two systems is available here.)

So, once I had the projections, I needed to come up with a measure of platoon tendencies. Since the available ZiPS projections only included one rate stat, batting average, I decided to use that as my measure of batting success. I computed platoon severity by taking the larger of a player’s BA against left-handers and BA against right-handers and dividing by the smaller of those two numbers. (As an example, Gomes’s BA against RHP is .222 and against LHP is .279, so his ratio is .279/.222 = 1.26.) My source for those data is FanGraphs.

I computed that severity for players with at least 500 PA against both left-handers and right-handers going into the season for which they were projected; for instance, for 2010 I would have used career data stopping at 2009. I then looked at their actual BA in the projected year, computed the deviation between that BA and the projected BA, and saw if there was any correlation between the deviation and the platoon ratio. (I actually used the absolute value of the deviation, so that magnitude was taken into account without worrying about direction.) Taking into account the availability of projections and requiring that players have at least 150 PA in the season where the deviation is measured, we have a sample size of 556 player seasons.

As it turns out, there isn’t any correlation between the two parameters. My hypothesis was that there’d be a positive correlation, but the correlation is -0.026 for Marcel projections and -0.047 for ZiPS projections, neither of which is practically or statistically significantly different from 0. The scatter plots for the two projection systems are below:

Marcel ZIPS

Now, there are a number of shortcomings to the approach I’ve taken:

  • It only looks at two projection systems; it’s possible this problem arises for other systems.
  • It only looks at batting average due to data availability issues, when wOBA, OPS, and wRC+ are better, less luck-dependent measures of offensive productivity.
  • Perhaps most substantially, we would expect the projection to be wrong if the player has a large platoon split and faces a different percentage of LHP/RHP during the season in question than he has in his career previously. I didn’t filter on that (I was having issues collecting those data in an efficient format), but I intend to come back to it.

So, if you’re looking for a takeaway, it’s that large platoon-split players on the whole do not appear to be poorly projected (for BA by ZiPS and Marcel), but it’s still possible that those with a large change in circumstances might differ from their projections.

The Shelf Life of Top Shelf Performances

Leave a reply

Short summary: I look at how much year-over-year persistence there is in the lists of best position players and pitchers, using Wins Above Replacement (WAR). It appears as though there is substantial volatility, with only the very best players being more likely than not to repeat on the lists. In the observed data, pitchers are slightly more likely to remain at the top of the league than position players, but the difference is not meaningful.

Last week, Sky Kalkman posted a question that I thought seemed interesting.

Obviously, this requires having a working definition of “ace,” for which Kalkman later suggests “the top dozen-ish” pitchers in baseball. That seems reasonable to me, but it raises another question: what metric to use for “top”?

I eventually wound up using an average of RA9-WAR and FIP-WAR (the latter being the standard WAR offered by FanGraphs). There are some drawbacks to using counting stats rather than a rate stat, specifically that a pitcher that misses two months due to injury might conceivably be an ace but won’t finish at the top of the leaderboard. That said, my personal opinion is that health is somewhat of a skill and dependability is part of being an ace.

I chose to use this blend of WAR (it’s similar to what Tangotiger sometimes says he uses) because I wanted to incorporate some aspects of Fielding Dependent Pitching into the calculations. It’s a bit arbitrary, but the analysis I’m about to present doesn’t change much if you use just FIP-WAR or plain old FIP- instead.

I also decided to use the period from 1978 to the present as my sample; 1978 was the expansion that brought the majors to 26 teams (close to the present 30), keeping the total pool of talent reasonably similarly-sized throughout the entire time period while still providing a reasonably large sample size.

So, after collecting the data, what did I actually compute? I worked with two groups—the top 12 and top 25 pitchers by WAR in a given year—and then looked at three things. I first examined the probability they would still be in their given group the next year, two years after, and so on up through 10 years following their initial ace season. (Two notes: I included players tied for 25th, and I didn’t require that the seasons be consecutive, so a pitcher who bounced in and out of the ace group will still be counted. For instance, John Smoltz counts as an ace in 1995 and 2005 in this system, but not for the years 2001–04. He’s still included in the “ace 10 years later” group.) As it turns out, the “half-life” that Kalkman postulates is less than a year: 41% of top 25 pitchers are in the top 25 the next year, with that figure dropping to 35% for top 12 pitchers who remain in the top 12.

I also looked at those probabilities by year, to see if there’s been any shift over time—basically, is the churn greater or less than it used to be? My last piece of analysis was to look at the probabilities by rank in the initial year to see how much more likely the very excellent pitchers are to stay at the top than the merely excellent pitchers. Finally, I ran all of these numbers for position players as well, to see what the differences are and provide some additional context for the numbers.

I played around and ultimately decided that some simple charts were the easiest way to convey what needed to be said. (Hopefully they’re of acceptable quality—I was having some issues with my plotting code.) We’ll start with the “half-life” graph, i.e. the “was this pitcher still an ace X years later?” chart.

HalfLife

As you can see, there’s a reasonable amount of volatility, in that the typical pitcher who cracks one of these lists won’t be on the same list the next year. While there’s a small difference between pitchers and position players for each group in the one year numbers, it’s not statistically significant and the lines blur together when looking at years further out, so I don’t think it’s meaningful.

Now, what if we look at things by year? (Note that from here on out we’re only looking at the year-over-year retention rate, not rates from two or more years.)

AllByYear

This is a very chaotic chart, so I’ll explain what I found and then show a slightly less noisy version. The top 25 groups aren’t correlated with each other, and top 25 batters isn’t correlated with time. However, top 25 pitchers is lightly positively correlated with time (r = 0.33 and p = 0.052), meaning that the top of the pitching ranks has gotten a bit more stable over the last 35 years. Perhaps more interestingly, the percentage for top 12 pitchers is more strongly positively correlated with time (r = 0.46, p < 0.01), meaning that the very top has gotten noticeably more stable over time (even compared to the less exclusive top), whereas the same number for hitters is negative (r = -0.35, p = 0.041), meaning there’s more volatility at the top of the hitting WAR leaderboard than there used to be.

These effects should be more visible (though still noisy) in the next two charts that show just the top 12 numbers (one’s smoothed using LOESS, one not). I’m reluctant to speculate as to what could be causing these effects: it could be related to run environments, injury prevention, player mobility, or a whole host of other factors, so I’ll leave it alone for now. (The fact that any explanation might have to also consider why this effect is stronger for the top 12 than the top 25 is another wrinkle.)

12ByYear

SmoothByYear

The upshot of these graphs, though, is that (if you buy that the time trend is real) the ace half-life has actually increased over the last couple decades, and it’s gone down for superstar position players over the same period.

Finally, here’s the chart showing how likely a player who had a given rank is to stay in the elite group for another year. This one I’ve also smoothed to make it easier to interpret:

RankPlot

What I take away from these charts are that, unsurprisingly, the very best players tend to persist in the elite group for multiple years, but that the bottom of the top is a lot less likely to stay in the group. Also, the gaps at the far left of the graph (corresponding to the very best players) are larger than the gaps we’ve seen between pitchers and hitters anywhere else. This says that, in spite of pitchers’ reputation as being volatile, at the very top they have been noticeably less prone to large one-year drop offs than the hitters are. That said, the sample is so small (these buckets are a bit larger than 30 each) that I wouldn’t take that as predictive so much as indicative of an odd trend.

A Little Bit on FIP-ERA Differential

1 Reply

Brief Summary:

Fielding Independent Pitching (FIP) is a popular alternative to ERA predicated on a pitcher’s strikeout, walk, and home run rates. The extent to which pitchers deserve credit for having FIPs better or worse than ERAs is something that’s poorly understood, though it’s usually acknowledged that certain pitchers do deserve that credit. Given that some of the non-random difference can be attributed to where a pitcher plays because of defense and park effects, I look at pitchers who change teams and consider the year-over-year correlation between their ERA-FIP differentials. I find that the correlation remains and is not meaningfully different from the year-over-year correlation for pitchers that stay on the same team. However, this effect is (confusingly) confounded with innings pitched.

 

After reading this Lewie Pollis article on Baseball Prospectus, I started thinking more about how to look at FIP and other ERA estimators. In particular, he talks about trying to assess how likely it is that a pitcher’s “outperforming his peripherals” (scare quotes mine) is skill or luck. (I plan to run a more conceptual piece on that FIP and other general issues soon.) That also led me to this FanGraphs community post on FIP, which I don’t think is all that great (I think it’s arguing against a straw man) but raises useful points about FIP regardless.

After chewing on all of that, I had an idea that’s simple enough that I was surprised nobody else (that I could find) had studied it before. Do pitchers preserve their FIP-ERA differential when they change teams? My initial hypothesis is that they shouldn’t, at least not to the same extent as pitchers who don’t change teams. After all, in theory (just to make it clear: in theory) most or much of the difference between FIP and ERA should be related to park and defensive effects, which will change dramatically from team to team. (To see an intuitive demonstration of this, look at the range of ERA-FIP values by team over the last decade, where each team has a sample of thousands of innings. The range is half a run, which is substantial.)

Now, this is dramatically oversimplifying things—for one, FIP, despite its name, is going to be affected by defense and park effects, as the FanGraphs post linked above discusses, meaning there are multiple moving parts in this analysis. There’s also the possibility that there’s either selection bias (pitchers who change teams are different from those who remain) or some treatment effect (changing teams alter’s a pitcher’s underlying talent). Overall, though, I still think it’s an interesting question, though you should feel free to disagree.

First, we should frame the question statistically. In this case, the question is: does knowing that a pitcher changed teams give us meaningful new information about his ERA-FIP difference in year 2 above and beyond his ERA-FIP difference in year 1. (From here on out, ERA-FIP difference is going to be E-F, as it is on FanGraphs.)

I used as data all consecutive pitching seasons of at least 80 IP since 1976. I’ll have more about the inning cutoff in a little bit, but I chose 1976 because it’s the beginning of the free agency era. I said that a pitcher changed teams if they played for one team for all of season 1 and another team for all of season 2; if they changed teams midseason in either season, they were removed from the data for most analyses. I had 621 season pairs in the changed group and 3389 in the same team group.

I then looked at the correlation between year 1 and year 2 E-F for the two different groups. For pitchers that didn’t change teams, the correlation is 0.157, which ain’t nothing but isn’t practically useful. In a regression framework, this means that the fraction of variation in year 2 E-F explained by year 1 E-F is about 2.5%, which is almost negligible. For pitchers who changed teams, the correlation is 0.111, which is smaller but I don’t think meaningfully so. (The two correlations are also not statistically significantly different, if you’re curious.)

Looking at year-to-year correlations without adjusting for anything else is a very blunt way of approaching this problem, so I don’t want to read too much into a null result, but I’m still surprised—I would have thought there would be some visible effect. This still highlights one of the problems with the term Fielding Independent Pitching—the fielders changed, but there was still an (extremely noisy) persistent pitcher effect, putting a bit of a lie to the term “independent” (though as before, there are a lot of confounding factors so I don’t want to overstate this). At some point, I’d like to thoroughly examine how much of this result is driven by lucky pitchers getting more opportunities to keep pitching than unlucky ones, so that’s one for the “further research” pile.

I had two other small results that I ran across while crunching these numbers that are tangentially related to the main point:

  1. As I suspected above, there’s something different about pitchers who change teams compared to those who don’t. The average pitcher who didn’t change teams had an E-F of -0.10, meaning they had a better ERA than FIP. The average pitcher who did change teams had an E-F of 0.05, meaning their FIP was better than their ERA. The swing between the two groups is thus 0.15 runs, which over a few thousand pitchers is pretty big. There’s going to be some survivorship bias in this, because having a positive ERA-FIP might be related to having a high ERA, which makes one less likely to pitch 80 innings in the second season and thus more likely to drop out of my data. Regardless, though, that’s a pretty big difference and suggests something odd is happening in the trade and free agency markets.
  2. There’s a strong correlation between innings pitched in both year 1 and year 2 and E-F in year two for both groups of pitchers. Specifically, each 100 innings pitched in year 1 is associated with a 0.1 increase in E-F in year 2, and each 100 innings pitched in year 2 is associated with a 0.2 decrease in E-F in year 2. I can guess that the second one is happening because lower/negative E-F is going to be related to low ERAs, which get you more playing time, but I find the first part pretty confusing. Anyone who has a suggestion for what that means, please let me know.

So, what does this all signify? As I said before, the result isn’t what I expected, but when working with connections that are this tenuous, I don’t think there’s a clear upshot. This research has, however, given me some renewed skepticism about the way FIP is often employed in baseball commentary. I think it’s quite useful in its broad strokes, but it’s such a blunt instrument that I would advise being wary of people who try to draw strong conclusions about its subtleties. The process of writing the article has also churned up some preexisting ideas I had about FIP and the way we talk about baseball stats in general, so stay tuned for those thoughts as well.

More on Stealing with Runners on the Corners

Leave a reply

A few people kicked around some suggestions about my last piece on Tom Tango’s blog, so I’m following up with a couple more pieces of analysis that will hopefully shed some light on things. As a quick refresher, I looked at steal attempts with runners on the corners and found that the success rate is much larger than the break even point, especially with two outs. My research suggests teams are too conservative, i.e. they should send the runners more. For more about methods and data, look at the prior piece.

One initial correction from Tango is that I was treating one class of events improperly; that’s since been corrected. (Specifically, two out events where one runner is out and the other scores are now counted as successes, not failures.) Another point made by Peter Jensen is that I should consider what happens when the runners are moving and contact is made; that’s going to require a bit more grinding with the data, but it’s now on my list of things to look at.

Next, there were some questions about how much of the success rate is due to having abnormally good or bad runners. Here are two plots showing all successes and failures by the stolen base percentages of the runners on first and third. The first is for all situations, the second for two out situations only.

Quick data note: to compute attempts and stolen base percentage, I used a centered three-year average, meaning that if an attempt took place in 2010 the SB% fed in would be the aggregate figure from 2009–2011. These charts only include situations where both runners have at least 20 attempts.

All Situations Two Outs

To simplify the charts a bit, I put the attempts into one of 36 buckets based on the SB% of the runners and then computed the success rates for those buckets; you can see the results in the tables below. The bucket boundaries are based on the distribution of SB%, so the 17th, 33rd, 50th, 67th, and 83rd percentiles. Sample sizes are roughly 55 for two outs (minimum 40) and 100-110 overall (minimum 73).

Outcomes of 1st/3rd Steal Attempts by SB% of Runners on Base, All Situations
Third Base SB% Bucket
1st Base SB% Bucket 27.3%—61.4% 61.4%—68% 68%—72.5% 72.5%—75.8% 75.8%—80% 80%—95.5%
33.3%—64.9% 72.6 79.1 83.0 77.1 83.3 81.0
64.9%—70.6% 80.3 85.6 80.8 88.2 86.8 87.1
70.6%—74.4% 86.4 84.0 83.7 87.3 85.3 86.3
74.4%—77.6% 85.6 85.9 91.4 86.4 92.7 89.8
77.6%—81.2% 91.3 90.5 83.3 90.3 95.2 90.6
81.2%—96.2% 90.8 84.9 89.4 90.8 93.6 89.1
Outcomes of 1st/3rd Steal Attempts by SB% of Runners on Base, Two Outs
Third Base SB% Bucket
1st Base SB% Bucket 27.3%—60.9% 60.9%—67.6% 67.6%—72.1% 72.1%—75.5% 75.5%—80% 80%—93.9%
35%—64.1% 86.9 89.2 87.7 84.6 92.5 89.4
64.1%—70.1% 89.6 93.2 89.1 89.1 87.8 91.5
70.1%—74% 92.7 85.7 91.7 96.6 93.3 91.5
74%—77.5% 94.1 93.3 92.9 94.6 100.0 93.5
77.5%—81.1% 95.0 87.7 94.4 93.5 98.2 97.1
81.1%—95.5% 95.8 89.3 90.7 91.2 95.7 95.5

As you can see, even with noticeably below-average runners at both bases (average SB% is 70%), teams are successful so often that they should be trying it more often—all buckets but one in the two tables have a success rate above break-even. (BE rates are 75.5% overall and 69% for 2 outs.) There’s still a little bit of selection bias, which is pertinent, though I don’t think it accounts for most of the effect—see the note below. However, the fact that every single bucket comes in well above the break-even rate suggests to me that even accounting for the selection bias, this is still an area where managers should be more aggressive. At the very least, it seems that if there are two average base thieves on and two out, the runner on first should be going much more frequently than the current sub-10% attempt rate.

Note: One important thing to consider is that putting the attempts minimum in place noticeably increases the success rate—from 83% to 86% overall, and from 90% to 92% for two out situations. (The explanation for that is that really slow players don’t necessarily have poor SB%, they just have next to no stolen base attempts, so they are falling out of the data.) However, if you stick to the attempts where one or both runners have few attempts, the success rate only drops about 2 percentage points, which is still pretty far above the breakeven point overall and with two outs.

Stealing an Advantage from First and Third

1 Reply

(Note: Inspired by this post from Jeff Fogle, I decided to change the format up a bit for this post, specifically by putting an abstract at the beginning. We’ll see if it sticks.) This post looks at baserunning strategy with runners on first and third, specifically having to do with when to have the runner on first attempt to steal. My research suggests that teams may be currently employing this strategy in a non-optimal manner. While they start the runner as often as they should with one out, they should probably run more frequently with zero and two outs with runners on first and third than they currently. The gain from this aggressiveness is likely to be small, on the order of a few runs a season. Read on if you want to know how I came to this conclusion.

Back when I used to play a lot of the Triple Play series, I loved calling for a steal with runners on first and third. It seemed like you could basically always get the runner to second, and if he drew a throw then the runner on third would score. It’s one of those fun plays that introduced a bit of chaos and works disproportionately frequently in videogames. Is that last statement true? Well, I don’t know how frequently it worked in Triple Play 99, but I can look at how frequently it works in the majors. And it appears to work pretty darn frequently.*

* I haven’t found any prior research directly addressing this, but this old post by current Pirates analytics honcho Dan Fox obliquely touches on it. I’m pretty confident that his conclusions are different because he’s omitting an important case and focusing directly on double steals, and not because either one of us is wrong.

The data I looked at were Retrosheet play-by-play data from 1989–2013, looking at events classified as caught stealing, stolen bases, balks, and pickoffs with runners at first and third. I then removed caught stealing and steals where the runner on first remained on first at the end of the play, leaving 8500 events or so. That selection of events is similar to what Tom Tango et al. do in The Book and control for the secondary effects of base stealing, but I added the restriction about the runner on first to remove failed squeezes, straight steals of home, and other things that aren’t related to what we’re looking at. This isn’t going to perfectly capture the events we want, but modulo the limitations of play-by-play data it’s the best cut of the data I could think of. (It’s missing two big things: the impact of running on batter performance and what happens when the runners go and the ball is put in play. The first would take a lot of digging to guess at, and the second is impossible to get from my data, so I’m going to postulate they have a small effect and leave it at that.)

So, let’s say we define an outcome to be successful if it leads to an increased run expectancy. (Run expectancy is computed empirically and is essentially the average number of runs scored in the remainder of an inning given where the baserunners are and how many outs there are.) In this particular scenario, increased run expectancy is equivalent to an outcome where both runners are safe, which occurs 82.7% of the time. For reference, league average stolen base percentage over this period is 69.9% (via the Lahman database), so that’s a sizeable difference in success rates (though the latter figure doesn’t account for pickoffs, errors, and balks). (For what it’s worth, both of those numbers have gone up between 4 and 6 percentage points in the last five years.)

How much of that is due to self-selection and how much is intrinsic to the situation itself? In other words, is this just a function of teams picking their spots? It’s hard to check every aspect of this (catcher, pitcher, leverage, etc.), so I chose to focus on one, which is the stolen base percentage of the runner on first. I used a three year centered average for the players (meaning if the attempt took place in 1999, I used their combined stolen base figures from 1998–2000), and it turns out that on aggregate runners on first during 1st and 3rd steal attempts are about one percentage point better than the league average. That’s noticeable and not meaningless, but given how large the gap in success rate is the increased runner quality can’t explain the whole thing.

Now, what if we want to look at the outcomes more granularly? The results are in the table below. (The zeros are actually zero, not rounded.)

Outcomes of 1st/3rd Steal Attempts (Percentage)
Runner on First’s Destination
Runner on Third’s Destination Out 1st Base 2nd Base 3rd Base Run
Out 0.20 0.97 2.78 0.23 0.00
3rd Base 12.06 0.00 69.89 0.00 0.00
Run 1.07 0.36 9.31 2.98 0.15

This doesn’t directly address run expectancy, which is what we need if we’re going to actually determine the utility of this tactic. If you take into account the number of outs, balks, and pickoffs and combine the historical probabilities seen in that table with Baseball Prospectus’s 2013 run expectancy tables*, you get that each attempt is worth about 0.07 runs. (Restricting to the last five years, it’s 0.09.) That’s something, but it’s not much—you’d need to have 144 attempts a year at that success rate to get an extra win, which isn’t likely to happen given that there only about 200 1st and 3rd situations per team per year according to my quick count. Overall, the data suggest the break even success rate is on the order of 76%.**

* I used 2013 tables a) to simplify things and b) to make these historical rates more directly applicable to the current run environment.

** That’s computed using a slight simplification—I averaged the run values of all successful and unsuccessful outcomes separately, then calculated the break even point for that constructed binary process. Take the exact values with a grain of salt given the noise in the low-probability, high-impact outcomes (e.g. both runners score, both runners are out).

There’s a wrinkle to this, though, which is that the stakes and decision making processes are going to be different with zero, one, or two outs.  In the past, the expected value of running with first and third is actually negative with one out (-0.04), whereas the EV for running with two outs is about twice the overall figure. (The one out EV is almost exactly 0 over the last five years, but I don’t want to draw too many conclusions from that if it’s a blip and not a structural change.) That’s a big difference, probably driven by the fact that the penalty for taking the out is substantially less with two outs, and it’s not due to a small sample—two out attempts make up more than half the data. (For what it’s worth, there aren’t substantive discrepancies in the SB% of the runners involved between the different out states.) The table below breaks it down more clearly:

Success and Break Even Rates for 1st/3rd Steal Attempts by Outs
Number of Outs Historical Success Percentage Break Even Percentage
0 81.64 74.61
1 73.65 78.00
2 88.71 69.03
Overall 82.69 75.52

That third row is where I think there’s a lot of hay to be made, and I think the table makes a pretty clear case: managers should be quite aggressive about starting the runner if there’s a first and third with two outs, even if there’s a slightly below average runner at first. They should probably be a bit more aggressive than they currently are with no outs, and more conservative with one out.

There’s also plenty of room for this to happen more frequently; with two outs, the steal attempt rate last year was about 6.6% (it’s 5% with one out, and 4% with no outs). The number of possible attempts per team last year was roughly 200, split 100/70/30 between 2/1/0 outs, so there are some reasonable gains to be made. It’s not going to make a gigantic impact, but if a team sends the runner twice as often as they have been with two outs (about one extra time per 25 games), that’s a run gained, which is small but still an edge worth taking. Maybe my impulses when playing Triple Play had something to them after all.

A Look at Pitcher Defense

1 Reply

Like most White Sox fans, I was disappointed when Mark Buehrle left the team. I didn’t necessarily think they made a bad decision, but Buehrle is one of those guys that makes me really appreciate baseball on a sentimental level. He’s never seemed like a real ace, but he’s more interesting: he worked at a quicker pace than any other pitcher, was among the very best fielding pitchers, and held runners on like few others (it’s a bit out of date, but this post has him picking off two batters for each one that steals, which is astonishing).

In my experience, these traits are usually discussed as though they’re unrelated to his value as a pitcher, and the same could probably be said of the fielding skills possessed by guys like Jim Kaat and Greg Maddux. However, that’s covering up a non-negligible portion of what Buehrle has brought to his teams over the year; using a crude calculation of 10 runs per win, his 87 Defensive Runs Saved are equal to about 20% of his 41 WAR during the era for which have DRS numbers. (Roughly half of that 20% is from fielding his position, with the other half coming from his excellent work in inhibiting base thieves. Defensive Runs Saved are a commonly used, all-encompassing defensive metric from Baseball Info Solutions. All numbers in this piece are from Fangraphs. ) Buehrle’s extreme, but he’s not the only pitcher like this; Jake Westbrook had 62 DRS and only 18 WAR or so in the DRS era, which means the DRS equate to more than 30% of the WAR.

So fielding can make up a substantial portion of a pitcher’s value, but it seems like we rarely discuss it. That makes a fair amount of sense; single season fielding metrics are considered to be highly variable for position players who will be on the field for six times as many innings as a typical starting pitcher, and pitcher defensive metrics are less trustworthy even beyond that limitation. Still, though, I figured it’d be interesting to look at which sorts of pitchers tend to be better defensively.

For purposes of this study, I only looked at what I’ll think of as “fielding runs saved,” which is total Defensive Runs Saved less runs saved from stolen bases (rSB). (If you’re curious, there is a modest but noticeable 0.31 correlation between saving runs on stolen bases and fielding runs saved.) I also converted it into a rate stat by dividing by the number of innings pitched and then multiplying by 150 to give a full season rate. Finally, I restricted to aggregate data from the 331 pitchers who threw at least 300 innings (2 full seasons by standard reckoning) between 2007 and 2013; 2007 was chosen because it’s the beginning of the PitchF/X era, which I’ll get to in a little bit. My thought is that a sample size of 330 is pretty reasonable, and while players will have changed over the full time frame it also provides enough innings that the estimates will be a bit more stable.

One aside is that DRS, as a counting stat, doesn’t adjust for how many opportunities a given fielder has, so a pitcher who induces lots of strikeouts and fly balls will necessarily have DRS values smaller in magnitude than another pitcher of the same fielding ability but different pitching style.

Below is a histogram of pitcher fielding runs/150 IP for the population in question:

Histogram

If you’re curious, the extreme positive values are Greg Maddux and Jake Westbrook, and the extreme negative values are Philip Humber, Brandon League, and Daniel Cabrera.

This raises another set of questions: what sort of pitchers tend to be better fielders? To test this, I decided to use linear regression—not because I want to make particularly nuanced predictions using the estimates, but because it is a way to examine how much of a correlation remains between fielding and a given variable after controlling for other factors. Most of the rest of the post will deal with the regression methods, so feel free to skip to the bold text at the end to see what my conclusions were.

What jumped out to me initially, is that Buehrle, R.A. Dickey, Westbrook, and Maddux are all extremely good fielding pitchers that aren’t hard throwers; to that end, I included their average velocity as one of the independent variables in the regression. (Hence the restriction to the PitchF/X era.) To control for the fact that harder throwers also strike out more batters and thus don’t have as many opportunities to make plays, I included the pitcher’s strikeouts per nine IP as a control as well.

It also seems plausible to me that there might be a handedness effect or a starter/reliever gap, so I added indicator variables for those to the model as well. (Given that righties and relievers throw harder than lefties and starters, controlling for velocity is key. Relievers are defined as those with at least half their innings in relief.) I also added in ground ball rate, with the thought that having more plays to make could have a substantial effect on the demonstrated fielding ability.

There turns out to be a noticeable negative correlation between velocity and fielding ability. This doesn’t surprise me, as it’s consistent with harder throwers having a longer, more intense delivery that makes it harder for them to react quickly to a line drive or ground ball. According to the model, we’d associate each mile per hour increase with a 0.2 fielding run per season decrease; however, I’d shy away from doing anything with that estimate given how poor the model is. (The R-squared values on the models discussed here are all less than 0.2, which is not very good.) Even if we take that estimate at face value, though, it’s a pretty small effect, and one that’s hard to read much into.

We don’t see any statistically significant results for K/9, handedness, or starter/reliever status. (Remember that this doesn’t take into account runs saved through stolen base prevention; in that case, it’s likely that left handers will rate as superior and hard throwers will do better due to having a faster time to the plate, but I’ll save that for another post.) In fact, of the non-velocity factors considered, only ground ball rate has a significant connection to fielding; it’s positively related, with a rough estimate that a percentage point increase in groundball rate will have a pitcher snag 0.06 extra fielding runs per 150 innings. That is statistically significant, but it’s a very small amount in practice and I suspect it’s contaminated by the fact that an increase in ground ball rate is related to an increase in fielding opportunities.

To attempt to control for that contamination, I changed the model so that the dependent (i.e. predicted) variable was [fielding runs / (IP/150 * GB%)]. That stat is hard to interpret intuitively (if you elide the batters faced vs. IP difference, it’s fielding runs per groundball), so I’m not thrilled about using it, but for this single purpose it should be useful to help figure out if ground ball pitchers tend to be better fielders even after adjusting for additional opportunities.

As it turns out, the same variables are significant in the new model, meaning that even after controlling for the number of opportunities GB pitchers and soft tossers are generally stronger fielders. The impact of one extra point of GB% is approximately equivalent to losing 0.25 mph off the average pitch speed; however, since pitch speed has a pretty small coefficient we wouldn’t expect either of these things to have a large impact on pitcher fielding.

This was a lot of math to not a huge effect, so here’s a quick summary of what I found in case I lost you:

  • Harder throwers contribute less on defense even after controlling for having fewer defensive opportunities due to strikeouts. Ground ball pitchers contribute more than other pitchers even if you control for having more balls they can make plays on.
  • The differences here are likely to be very small and fairly noisy (especially if you remember that the DRS numbers themselves are a bit wonky), meaning that, while they apply in broad terms, there will be lots and lots of exceptions to the rule.
  • Handedness and role (i.e. starter/reliever) have no significant impact on fielding contribution.

All told, then, we shouldn’t be too surprised Buehrle is a great fielder, given that he doesn’t throw very hard. On the other hand, though, there are plenty of other soft tossers who are minus fielders (Freddy Garcia, for instance), so it’s not as though Buehrle was bound to be good at this. To me, that just makes him a little bit quirkier and reminds me of why I’ll have a soft spot for him above-and-beyond what he got just for being a great hurler for the Sox.

Picking a Pitch and the Pace of the Game

Leave a reply

Here’s a short post to answer a straight-forward question: do pitchers that throw more pitches pitch more slowly? If it’s not clear, the idea is that a pitcher who throws several pitches frequently will take longer because the catcher has to spend more time calling the pitch, perhaps with a corresponding increase in how often the pitcher shakes off the catcher.

To make a quick pass at this, I pulled FanGraphs data on how often each pitcher threw fastballs, sliders, curveballs, changeups, cutters, splitters, and knucklers, using data from 2009–13 on all pitches with at least 200 innings. (See the data here. There are well-documented issues with the categorizations, but for a small question like this they are good enough.) The statistic used for how quickly the pitcher worked was the appropriately named Pace, which measures the number of seconds between pitches thrown.

To easily test the hypothesis, we need a single number to measure how even the pitcher’s pitch mix is, which we believe to be linked to the complexity of the decision they need to make. There are many ways to do this, but I decided to go with the Herfindahl-Hirschman Index, which is usually used to measure market concentration in economics. It’s computed by squaring the percentage share of each pitch and adding them together, so higher values mean things are more concentrated. (The theoretical max is 10,000.) As an example, Mariano Rivera threw 88.9% cutters and 11.1% fastballs over the time period we’re examining, so his HHI was 88.9^{2} + 11.1^{2} = 8026. David Price threw 66.7% fastballs, 5.8% sliders, 6.6% cutters, 10.6% curveballs, and 10.4% changeups, leading to an HHI of 4746. (See additional discussion below.) If you’re curious, the most and least concentrated repertoires split by role are in a table at the bottom of the post.

As an aside, I find two people on those leader/trailer lists most interesting. The first is Yu Darvish, who’s surrounded by junkballers—it’s pretty cool that he has such amazing stuff and still throws 4.5 pitches with some regularity. The second is that Bartolo Colon has, according to this metric, less variety in his pitch selection over the last five years than the two knuckleballers in the sample. He’s somehow a junkballer but with only one pitch, which is a pretty #Mets thing to be.

Back to business: after computing HHIs, I split the sample into 99 relievers and 208 starters, defined as pitchers who had at least 80% of their innings come in the respective role. I enforced the starter/reliever split because a) relievers have substantially less pitch diversity (unweighted mean HHI of 4928 vs. 4154 for starters, highly significant) and b) they pitch substantially slower, possibly due to pitching more with men on base and in higher leverage situations (unweighted mean Pace of 23.75 vs. 21.24, a 12% difference that’s also highly significant).

So, how does this HHI match up with pitching pace for these two groups? Pretty poorly. The correlation for starters is -0.11, which is the direction we’d expect but a very small correlation (and one that’s not statistically significant at p = 0.1, to the limit extent that statistical significance matters here). For relievers, it’s actually 0.11, which runs against our expectation but is also statistically and practically no different from 0. Overall, there doesn’t seem to be any real link, but if you want to gaze at the entrails, I’ve put scatterplots at the bottom as well.

One important note: a couple weeks back, Chris Teeter at Beyond the Box Score took a crack at the same question, though using a slightly different method. Unsurprisingly, he found the same thing. If I’d seen the article before I’d had this mostly typed up, I might not have gone through with it, but as it stands, it’s always nice to find corroboration for a result.

StartersRelievers

Relief Pitchers with Most Diverse Stuff, 2009–13
Name FB% SL% CT% CB% CH% SF% KN% HHI
1 Sean Marshall 25.6 18.3 17.7 38.0 0.5 0.0 0.0 2748
2 Brandon Lyon 43.8 18.3 14.8 18.7 4.4 0.0 0.0 2841
3 D.J. Carrasco 32.5 11.2 39.6 14.8 2.0 0.0 0.0 2973
4 Alfredo Aceves 46.5 0.0 17.9 19.8 13.5 2.3 0.0 3062
5 Logan Ondrusek 41.5 2.0 30.7 20.0 0.0 5.8 0.0 3102
Relief Pitchers with Least Diverse Stuff, 2009–13
Name FB% SL% CT% CB% CH% SF% KN% HHI
1 Kenley Jansen 91.4 7.8 0.0 0.2 0.6 0.0 0.0 8415
2 Mariano Rivera 11.1 0.0 88.9 0.0 0.0 0.0 0.0 8026
3 Ronald Belisario 85.4 12.7 0.0 0.0 0.0 1.9 0.0 7458
4 Matt Thornton 84.1 12.5 3.3 0.0 0.1 0.0 0.0 7240
5 Ernesto Frieri 82.9 5.6 0.0 10.4 1.1 0.0 0.0 7013
Starting Pitchers with Most Diverse Stuff, 2009–13
Name FB% SL% CT% CB% CH% SF% KN% HHI
1 Shaun Marcum 36.6 9.3 17.6 12.4 24.1 0.0 0.0 2470
2 Freddy Garcia 35.4 26.6 0.0 7.9 13.0 17.1 0.0 2485
3 Bronson Arroyo 42.6 20.6 5.1 14.2 17.6 0.0 0.0 2777
4 Yu Darvish 42.6 23.3 16.5 11.2 1.2 5.1 0.0 2783
5 Mike Leake 43.5 11.8 23.4 9.9 11.6 0.0 0.0 2812
Starting Pitchers with Least Diverse Stuff, 2009–13
Name FB% SL% CT% CB% CH% SF% KN% HHI
1 Bartolo Colon 86.2 9.1 0.2 0.0 4.6 0.0 0.0 7534
2 Tim Wakefield 10.5 0.0 0.0 3.7 0.0 0.0 85.8 7486
3 R.A. Dickey 16.8 0.0 0.0 0.2 1.5 0.0 81.5 6927
4 Justin Masterson 78.4 20.3 0.0 0.0 1.3 0.0 0.0 6560
5 Aaron Cook 79.7 9.7 2.8 7.6 0.4 0.0 0.0 6512

Boring methodological footnote: There’s one primary conceptual problem with using HHI, and that’s that in certain situations it gives a counterintuitive result for this application. For instance, under our line of reasoning we would think that, ceteris paribus, a pitcher who throws a fastball 90% of a time and a change 10% of the time would have an easier decision to make than one who throws a fastball 90% of the time and a change and slider 5% each. However, the HHI is higher for the latter pitcher—which makes sense in the context of market concentration, but not in this scenario. (The same issue holds for the Gini coefficient, for that matter.) There’s a very high correlation between HHI and the frequency of a pitcher’s most common pitch, though, and using the latter doesn’t change any of the conclusions of the post.

The Joy of the Internet, Pt. 2

Leave a reply

I wrote one of these posts a while back about trying to figure out which game Bunk and McNulty attend in a Season 3 episode of The Wire. This time, I’m curious about a different game, and we have a bit less information to go on, so it took a bit more digging to find.

The intro to the Drake song “Connect” features the call of a home run being hit. Given that it probably required getting the express written consent of MLB for this sample, my guess is that he got it recorded by an announcer in the studio (as he implies around the 10:30 mark of this video). Still, does it match any games we have on record?

To start, I’m going to assume that this is a major league game, though there’s of course no way of knowing for sure. From the song, all we get is the count, the fact that it was a home run, the direction of the home run, and the name of the outfielder.  The first three are easy to hear, but the fourth is a bit tricky—a few lyrics sites (including the description of the video I linked) list it as “Molina,” but that can’t be the case, as none of the Molinas who’ve played in the bigs played the outfield.

RapGenius, however, lists it as “Revere,” and I’m going to go with that, since Ben Revere is an active major league center fielder and it seems likely that Drake would have sampled a recent game. So, can we find a game that matches all these parameters?

I first checked for only games Revere has played against the Blue Jays, since Drake is from Toronto and the RapGenius notes say (without a source) that the call is from a Jays game. A quick check of Revere’s game logs against the Jays, though, says that he’s never been on the field for a 3-1 homer by a Jay.

What about against any other team? Since checking this by hand wasn’t going to fly (har har), I turned to play-by-play data, available from the always-amazing Retrosheet. With the help of some code from possibly the nerdiest book I own, I was able to filter every play since Revere has joined the league to find only home runs hit to center when Revere was in center and the count was 3-1.

Somewhat magically, there was only one: a first inning shot by Carlos Gomez against the Twins in 2011. The video is here, for reference. I managed to find the Twins’ TV call via MLB.TV, and the Brewers’ team did the MLB.com video, and (unsurprisingly) neither call fits the sample, though I didn’t go looking for the radio call. Still, the home run is such that it wouldn’t be surprising if either one of the radio calls matched what Drake used, or if it was close and Drake had it rerecorded in such a way that preserved the details of the play.

So, probably through dumb luck, Drake managed to pick a unique play to sample for his track. But even though it’s a baseball sample, I still click back to “Hold On, We’re Going Home” damn near every time I listen to the album.